IT導入のヒントブログ IT BLOG
【参加レポート】福岡ブロックチェーン勉強会#42(ブロックチェーンを支えるアルゴリズム) (その1)(ECDSA編)

こんにちは、スミリオンの長嶋です。
以下の勉強会に参加してきましたので、内容をレポートします。(その1)
福岡ブロックチェーン勉強会#42(ブロックチェーンを支えるアルゴリズム)
https://gbec.connpass.com/event/158117/
今回は、ブロックチェーンを支えるアルゴリズムと題し、「ECDSA」と「Schnorr 署名」について、中城さんに説明して頂きました。
ECDSAについて
ECDSAについては、以下のサイトなどをベースに説明して頂きました。
https://zoom-blc.com/what-is-ecdsa
ビットコインやイーサリアムなどのブロックチェーンネットワークにおいて、不正なく「正しい送信元から正しい相手に正しい送金額」を送るためにECDSAという暗号技術が用いられているそうです。
また、ECDSA(Elliptic Curve Digital Signature Algorithm)とは、楕円曲線DSAとも呼ばれビットコインやイーサリアムの文脈では特にトランザクションの署名に使われいるということで、まずは楕円曲線の説明から始まりました。
楕円曲線とは以下の方程式のこと
ECDSAを理解するための前提知識としてまずは楕円曲線上の演算を定義していきます。楕円曲線とは一般的に、以下のような方程式で表される曲線です。(上記のページから引用)
![]()
ビットコインやイーサリアムではsecp256k1曲線という形式が用いられているので、a=0, b=7として、以下のように表されるそうです。
![]()
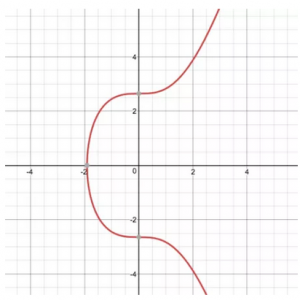
次に加算の定義について
まず、secp256k1曲線上でA+Bの加算をしたいときは以下のように点Aと点Bを通る直線を引き、曲線との交点のx軸に関する対称点がA+Bとなります。これが、楕円曲線上での加算の定義となります。(上記のページから引用)
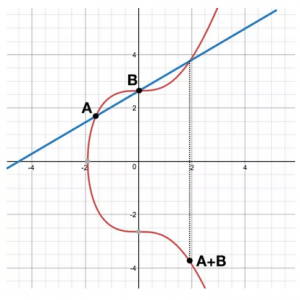
難しい説明は割愛しますが、上記のページから引用すると
どのような楕円曲線か、どのベースポイントGかはsecp256k1により定義されている上で、共通鍵rGから秘密鍵rを求めることがとても難しいのです。(これを楕円曲線上の離散対数問題と呼びます。)要は、ハッシュ関数のような一方向性の性質を持っています。
つまり、楕円曲線暗号ではこの離散対数問題の難しさを利用することで、「秘密鍵から公開鍵を生成するのは簡単だけれども、公開鍵から秘密鍵を求めることは極限に難しい」という状況を生み出していることになります。
と言う事らしいです。
次にECDSAの算出式と署名検証についての説明がありました
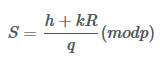

Qの検証
まず受け取ったトランザクションデータからハッシュ値hを算出し、以下のQを検証します。(上記のページから引用)


Qの検証結果
このQのx座標が受け取ったRと等しければ、正当な署名であると証明することができます。これは以下のような演算が行われます。(上記のページから引用)
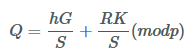
K=kGであり、S値を代入して計算すると、
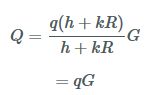
一通り説明が終わった後に、各自実際にK=kGやS値をQの検証の式に代入し、検証結果の答えになるかどうかの検算をしました。
学生以来でしたが、久しぶりに数学で頭をフル回転させた気がします。。。

中城さんの検算結果
「ECDSA」ですが、ブロックチェーンが普及する前からある暗号技術とのことで、他にも使用されているそうです。
例えば、sslの証明書など
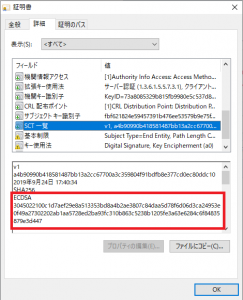
ちょっと内容が長くなってしまいましたので、「Schnorr 署名」については、別で投稿したいと思います。
■参考資料
どうしてECDSA署名から公開鍵が復元できるのか?
https://techmedia-think.hatenablog.com/entry/2018/01/21/131037